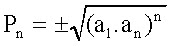Fonte http://profdrico.sites.uol.com.br
Progressão Geométrica
É uma sequência em que cada termo, a partir do segundo, é o produto do anterior com uma constante, denominada razão, representada pela letra 'q'.
Elementos
a1 : 1o termo
an : termo genérico, termo geral (ou n-ésimo termo)
q : razão
n : número de termos
Sn : soma dos termos
Pn : produto dos termos
an : termo genérico, termo geral (ou n-ésimo termo)
q : razão
n : número de termos
Sn : soma dos termos
Pn : produto dos termos
an = a1 . qn-1
Produtos dos Termos de uma P.G.
O produto dos 'n' termos de uma P.G. é dado por:
Soma dos Termos da P.G.
P.G. limitada (ou finita)
P.G. ilimitada (ou infinita) decrescente
Termo Médio de uma P.G.
TM2 = a1.an
Representação de 3 termos na P.G.
Para representar três termos em P.G., sendo dado o produto dos termos, use:
1) Calcule o primeiro termo de uma PG, sabendo que a9 = 1280 e q=2
(R:a1 =5)
(R:a1 =5)
2)Interpolar ou inserir três meios geométricos entre 3 e 48. (R: q= -2,+ 2)
3) Determine o número de termos da PG (1,2,.....256) (R:9)
4) Numa PG de doze termos o primeiro é igual a 5 e a razão é 2.Determine o ultimo termo. (R:a31= 10 240)
5) O numero x é positivo e os números 8, x e x + 6 formam, nessa ordem, uma progressão geométrica . calcule o x (R: 12)
6) Calcule a soma dos 6 primeiros termos da P.G. (7, 14, ...).
6) Calcule a soma dos 6 primeiros termos da P.G. (7, 14, ...).
(R: S6 = 441)